スーパーコンピュータ「富岳」の性能を最大限に活かす方法を探る −2020年ゴードン・ベル賞ノミネートの八代主任研究員に聞く(第1回)

【インタビュイー】
八代尚（地球システム領域 衛星観測研究室 主任研究員）

【インタビュアー】
地球環境研究センターニュース編集局
江守正多（地球システム領域 副領域長）

＊このインタビューは2021年5月11日に行われました。

ゴードン・ベル賞^*1は、計算機の専門家以外にはあまり知られておらず、一般の読者にとってなじみがあるものではありません。しかし、スーパーコンピュータを使った研究は、気候研究をはじめとして、今後ますます重要になるはずです。

今回は、スーパーコンピュータ「富岳」(図1)を使った気象計算^*2によって、2020年のゴードン・ベル賞のファイナリストに選ばれた八代尚主任研究員（スーパーコンピュータ「富岳」を利用した、史上最大規模の気象計算を実現－スパコン×シミュレーション×データ科学の協働が切り開く未来の気象予報－　https://www.nies.go.jp/whatsnew/20201120/20201120.html　を参照）に、その研究についてお聞きしました。

今回は、スーパーコンピュータについては素人のインタビュアーである編集局の中の人の心の声を（　）に入れた青字で記しています。

編集局：現在の天気予報のほとんどが数値予報を基盤としていると聞いています。数値予報の精度が上がれば天気予報はより当たるようになるのでしょうか。

八代：現在の天気予報が数値予報を基にしているというのはそのとおりで、結構前から、気象予報士さんが自分で天気図を描いて予報するよりも、コンピュータに任せたほうがよく当たるようになってきました。気象庁も数値予報モデルをずっと改良しつづけていて、さらに当たるようになった。天気予報の信頼性が昔よりも上がったのは、やはり、数値予報の精度を上げてきたことが一番大きいと思います。

もちろん、天気を知りたい時間から予報を始める時間が近いほど、たとえば30分前から予報したら当たりやすい。1日くらい前だと結構当たるけれども、2日くらい前に、「明後日雨降りそうだから…」といっても、実際気がついたら雨降らなかったね、ということがあったりして、数日先の天気予報は、まだ当たらないこともあるというのが現状だとは思いますね。

数値予報というものは、空気の流れを計算するだけではなくて、雲が生まれて大きくなって雨が降るとか、地面の周りで風が渦巻くみたいな現象をうまく表現してやらないと、どんどんずれが大きくなっていって、1日先、2日先、3日先…とシミュレーションの結果が現実から離れていってしまう。現在の天気予報のシミュレーションは完璧ではないというのが、実際のところだと思います。

編集局：なぜシミュレーションは完璧ではないのか、説明していただけるとありがたいです。
（数値予報の精度が上がれば予報は当たるといいながら、「シミュレーションは完璧ではない」とは、話が矛盾しているのでは？と早くも不思議に思う編集局。）

八代：まず、計算機で計算したから結果が全部正しいと思うのは、やめたほうがいいです。

ある情報を入力して、人間がプログラムしたとおりにコンピュータが計算して結果が出てくる、というときには、いろんなところに間違い、というか、誤差が存在しています。第一に、入力した情報が完璧ではないはずです。世界中の、今現在の天気の状態を、事細かに知ることには自ずと限界があります。

第二に、シミュレーションそのもの、モデルそのものについても、計算式が全部正しいとしても、現実を全部表現できるわけではないということがあります。式の中に、まだ足りない要素があるのかもしれない。それに、方程式で表される現象を、コンピュータの中で計算できるように作り変えるときに、離散化^*3という操作が入るのですが、そうするとたいてい結果が「正しくなくなってしまう」んです。

誤差が生まれる大きな理由の一つは、コンピュータの中で計算するとき、連続してつながっている地球の大気を細かく区切って、その区切ったボックスごとに計算するようなことをしているのですが、その区切りサイズで結果が変わってきてしまうということです。

地球はとても広いので、地球の表面を細かく区切ったボックスで覆うようにするとき、ボックスのサイズをどのくらいにするかで、計算量が大きく変わってきます。昔は、地球の表面を1万～数万個くらいに区切り、鉛直（高さ）方向に大気層を分割していました。つまり、全部で100万個くらいのボックスに分けていたのですが、それだと分割のしかたが粗くて、東京と横浜が同じボックスに入るようなサイズなので、東京と横浜の天気を分けて考えることができないんです。すると私たちが体感的に思っている天気と全然合わない。そうなると、このシミュレーションの結果は合ってない、という気持ちになりますよね。

それに、天気予報のシミュレーションで使っている計算式は、風が風に、つまり風速が風に乗って移動するような式（項）が入っているのですが、これは非線形な方程式^*4で、次の状態を予想するのが難しくなる、つまり「解析的に解けない^*5」のです。

その場合、次の大気がどうなるかを予測するのに、空間だけでなく、時間もある程度短く区切って、そのなかで次の状態を計算していくということを繰り返す必要が出てきます。式変形だけでは、明日の天気がわからないので、コンピュータを使って、数分先とか10分先とかの状態を、順番に計算して積み重ねていくことで、時間を進めていくわけです。そうすると、ずれがあるとそれも積み重なっていき、空間的にもどんどん広がっていくので、2日先、3日先のシミュレーションの結果はさらに大きくずれていく、ということになります。
（時間や空間のボックスを細かく区切り、それらを少しずつ積み重ねて時間的・空間的な変化を予測すると、どうしてもずれが生じてしまう。さらに、時間や空間のボックスをどれほど細かく区切っても、そういったずれは出てしまう、ということが理解できたような気がしました。）

編集局：今回の論文では、時間も空間もかなり細かく区切って計算していらっしゃるということなので、どのくらい細かく区切ったかについて、一般的な区切り方と比べて説明していただけますか。

八代：世界中の気象機関の人たちは、大気のシミュレーションをするとき、いろいろなメッシュサイズ（空間的な区切りの大きさ）で計算をしています。たとえば日本の気象庁は、地球全体（全球）について、20kmメッシュくらいで計算しています。でも、日本の周りだけはもっと細かく計算しようと、日本列島の近くだけ５kmとか２kmとかのメッシュサイズでシミュレーションしています。こうして解像度を上げると、必然的に計算量が莫大になるので、日本列島付近だけメッシュサイズを細かくし、それ以外は細かい計算をしないことで全体の計算量を減らしているのです。

今回の論文のスーパーコンピュータ「富岳」によるシミュレーションは、全球すべて3.5kmメッシュという解像度で行っています。だいたい解像度が２倍に上がる、たとえば20kmが10kmになると、格子の点の数が4倍になります。格子の点の数が水平方向だけで4倍くらいになると、計算する時間の刻みを半分にしないとうまく計算できないので、それでさらに2倍になり、結局全部で8倍くらいの計算量になる。つまり、解像度が倍になると計算量が8倍（２の3乗倍）になるのです。今の気象庁の計算を20km格子とすると、今回行った3.5kmの格子というのは、解像度がだいたい6倍ですよね。そうすると６の3乗、つまり、200倍くらい計算量が多いということになります。

それから、時間刻みに関してはすごく短くて、１ステップが8秒です。

編集局：なぜ8秒にしたのですか。

八代：風を計算するときに、隣の隣の点まで、ボックスだったら隣の隣のボックスまで、１ステップの間に風が進んでしまうと、計算が不安定になって破綻します（クーラン条件^*6）。それを防ぐためには、時間刻みを短くして、風による１ステップあたりの移動距離を短くする必要がある。だから、解像度を半分にすると、時間間隔も半分にしないといけないわけです。それで、安定して計算できるぎりぎりが、今回は8秒だったということです。

編集局：１ステップ＝8秒という数値はどうやって出したのですか。

八代：一般的な風速と点の間隔から計算すればできますが、それだけではなくて、モデルの中のいろいろなノイズを加味して、実際に走らせてみて、ちゃんと安定して走る時間間隔をとることにしています。ときには、何コンマ何秒まで細かく調整する人もいますが、通常はそこまでしないで、60分＝3600秒を割り切れる秒数にすることが多いですね。
（単に細かくするのではなく、後の計算のことも考えて、ステップの秒数を割り出すのかと感心してしまいました。）

編集局：それにアンサンブル^*7計算が加わるということですね。アンサンブルについては、ご存じない方も多いと思いますので、説明していただけますか。
（アンサンブルについては、最近、あちこちで言及されているので、ぜひお聞きしたいと考えていました。）

八代：先ほど、シミュレーションが完璧ではないという話をしました。では、どのくらいずれるのかを調べる方法として、初期入力データの値をちょっとずつずらして、1日後、2日後などの計算結果を見るというやり方があります。今回、データ同化（後述。第2回の*1を参照）は6時間後で様子を見ているのですが、6時間後のシミュレーションに初期入力の違いがどのくらい出るかを調べて、統計的に、どの程度そのシミュレーションが確からしいかということを確認しています。

編集局：それは、初期入力による結果の「ずれ」がどのくらい出るかということですか。

八代：そうです。最初の入力値の違いによって6時間後の計算結果が、どのくらいずれているか、ということです。これが初期値アンサンブルという方法です。

アンサンブルの方法は、結構いろいろあって、初期値は同じだけれども、モデルのパラメータだけちょっとずらして、結果がどう変わるかを見るという方法もあるし、モデルそのものを複数集めてきて、初期値は一緒だけれども、違うモデルを走らせたら結果がどうなるかを見るものもあります。

気候の実験ではさまざまなアンサンブルを使います。ミップ（MIP）と呼ばれる、マルチモデル・インターコンパリスン・プロジェクト（Multi-model Intercomparison Project）が代表的なものです。CがつくとCMIP（Coupled Model Intercomparison Project）で大気海洋結合系、Atmosphere（大気）だけのAMIP（Atmospheric Model Intercomparison Project)も、Ocean（海洋）だけのOMIP（Ocean Model Intercomparison Project)もあります。Land（土地）に関するLS3MIP (Land Surface, Snow and Soil moisture Model Intercomparison Project)というのもあります。

編集局：今回はどのようなアンサンブルを使用しているのですか。

八代：初期値アンサンブルです。同じモデルと、同じ境界条件、同じパラメータを使って初期値だけ変えています。
（できるだけ正確な予測を出すために、計算する時間と空間をできるだけ細かく区切る、初期値アンサンブルを用いて計算結果を確率的に捉える、といったさまざまな工夫をしていることがわかります。なかでもアンサンブルは重要な役割を果たしているのですが、それがなぜ重要なのかについては、だんだんと明らかになってきます。）

編集局：なぜ、こういうアンサンブルを使うのですか。

八代：天気予報にも初期値が正しくない場合があるかもしれません。今回は全球3.5kmメッシュだから、水平で約1億点、3次元だと約100億点のデータの入力点がありますが、その全部に計算式であるモデルの入力値となる観測データがあるわけではないのです。あやしい初期値もいっぱいあるわけですよ。その初期値をちょっとずらして計算したら、どのくらい結果がずれてくるか。つまり、初期値が合っていないと思われるから、その「合ってなさ」が6時間後にどういうふうに影響するか？どういう幅で現れるか？ということを、知ることができる。

たとえば、モデルを一つ走らせてみて「2日後に雨が降りました」という結果が出たとします。とはいえ、本当は降っていないかもしれない。でも、初期値アンサンブルで計算した結果ならば、統計的に（確率的に）扱うことができます。

編集局：それが、「当たる」確率を上げるということですか。たくさん初期値を入れて計算することによって、何が「よくなる」のかをもう少しくわしく教えていただきたいのですが。

八代：単純な予報として、雨が「降るかもしれない」「降らないかもしれない」という結果が、2回計算して1回ずつ出たとします。そうすると「いったい、どっちなんだ」ということになりますよね。

では、それを100回やったとします。「降った」のが30回、「降らなかった」のが70回だとすると、結果が五分五分ではなかったことがわかります。サンプル数を増やすことによって、統計的に、よりrobustな（しっかりとした）結果を得ることができる。

編集局：それがなぜrobustだといえるのかがよくわからないのです。よく統計的に「有意に差が出る」とか「有意に何とか」っていいますよね。それがrobustということに関係すると思うのですけれど、どのくらい変わるとrobustになるのでしょうか。そういう目安とか、計算方法とか、理論とかがあるのかな、と考えてはいるのですが。

八代：たくさん計算して、結果がどんどんばらつく場合は、もっとたくさんやらないと、どれが正しいかわかりませんよね。でも、たくさん計算して、その結果がだんだん数として収束してくると、そのくらいの範囲に収まるということがわかってくる。

たとえば降水量だけ見て、100回計算して、だいたい平均値が100mm降るというところに収まったら、より確からしいってことになりますよね。でも、100回やっても、1000mmから0mmまでどれもランダムで降るようだと、何回やっても「あ、わかりませんね」っていうことになる。

編集局：それはつまり、計算結果が標準偏差(図2)のグラフの「山」のような形、理想的には正規分布(図3)みたいな形で出てくるということですか。

八代：はい。

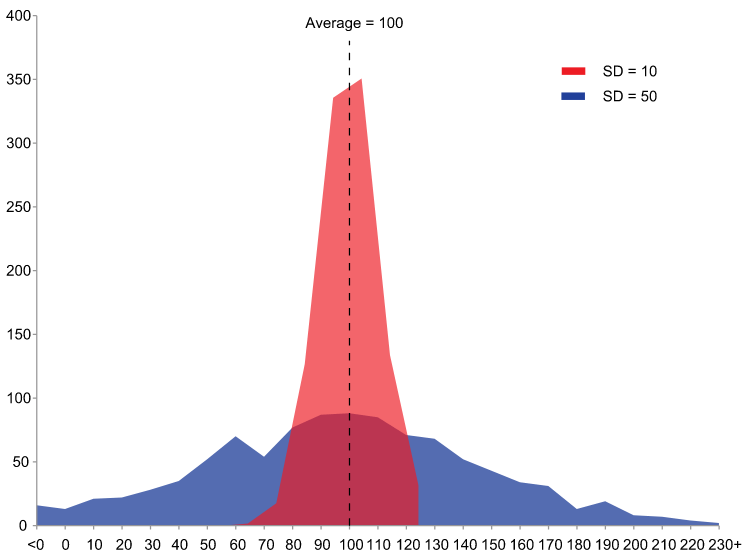
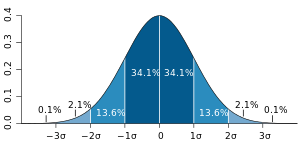
編集局：なるほど。そうすると、何がいえるのでしょうか。

八代：予報の確からしさとして、たとえば、ランダムに、100mm降るのかどうかもわからないという結果になったら、天気予報する側からいえば、「なんだかわかりません」ということしかいえない。でも、標準偏差の正規分布に近い形になったら、100mm降るのが一番確からしいので、自信をもって「100mm降りそうだ」といえることになります。

江守：予測の難しさ自体がわかるといったらいいのではないかと思いますが…。
（まだ腑に落ちていない様子の編集局を見て、江守副領域長が助け舟を出してくれました。）

編集局：予測の難しさ自体がわかるとはどういうことですか。

江守：ある日の天気は、何回計算しても、だいたいあるところに計算結果が集まってくる。ところが、別の日の天気は、何回計算しても、こういう答えも、ああいう答えも出てきてしまう。そういう日の天気は、本質的に、誰がやっても予測が難しい日なのですよ。計算結果が収束してくる日と、計算結果がばらばらになってしまう日とがある。

編集局：なぜ、そういうことが起こるのですか。

江守：それは、「カオスのアトラクタのどこを通っているか」（インタビュー記事の後ろにあるコラムを参照）によるんです。

八代：たくさん計算したからといって、正しい答えにたどり着く確率が上がるわけではないのですね。

編集局：それはいつも不思議に感じていたことです。今、江守さんがおっしゃったように、ある日は、どこを取っても結果が分散して、標準偏差のグラフにおけるような「山」の形にならない。でも、そうでないときは、幅の狭い一つの「山」の形がクリアに現れる、ということですか。

江守：たとえば、ある低気圧があって、もう、明日はこれがこういうふうに動くしかない、みたいな日は、何回計算しても、同じような答えが出てきたりする。だけど、微妙な弱い低気圧があって、それがどっちに動くかわからないとか、こちらに来るかもしれないけれど、来たときに、上空が寒いかどうかによって、天気が変わってくる…みたいな、そういう微妙な日があるわけですよね。

編集局：それはどのような条件によって決まるのですか。

江守：その日の気圧配置の特徴で決まります。そういう（結果が幅の狭い一つの「山」の形にならない）日は、たくさん計算しても、晴れという答えと雨という答えが出てきて、結果が一か所にあまり固まらないということではないかと。ぼくは天気予報をやっていないので、これは、ぼくなりのイメージですけれど。

だから、何回やっても結果が固まってくる日は、その天気になる確からしさが高いということが、たくさんアンサンブルをやればやるほど明確になる。

編集局：それでは、計算結果が集まってくる場合は、そのモデルが、うまく働いているっていうことを示す。でも、幅の狭い一つの「山」の形がうまく出てこないときは、そのモデルだとこれはうまく出てこない、あるいは、先ほどおっしゃっていたように、カオスのアトラクタの通るところがまずい、ということですか。

江守：通る場所がまずいというよりは、たまたまその日がそういう日だということ。たぶん、モデルによって性能の良し悪しはあるけれども、そういう日は、どのモデルでやっても、答えがばらつくんです。

編集局：では、モデルは、カオスのアトラクタのどこを通るかによって、うまく働く場合と働かない場合があるということですか。

江守：そうです。ただ、それが「どこを通るか」というのは、その日の天気が「たまたまどこにいるか」なんですよ。
（ここまできて、編集局にもアンサンブルがもつ意味がようやくわかってきました。）

八代：ローレンツ^*8という人が、これについていろいろ研究しています、彼は、たった3つの、次の時刻どうなるかという非線形方程式を並べ、その計算をして、初期値の、0.0000…の16桁目が1個違うだけで、その後のある時刻の結果が全然違う結果になってしまうということを証明したのです。

ローレンツ・アトラクタの図（コラムの図はその一例）を見てもらうとわかるのですが、この式では結果が突拍子もない値になることはないのです。でも、動きが非周期的なので特定の時間を取り出すと全然違う位置にいる、ということが起こります。つまり、きちんとわかっている式で、きちんと目に見えている数字を入れているにもかかわらず、その最後の桁の数字が１違うだけで結果が全然変わる。桁がある数字を扱っている以上は、どうやっても「ずれ」が生じるっていうことを証明してしまった…。

編集局：それはすごい！
（これには本当にびっくりしました。言葉で説明するのも相当に困難なことを、たった３つのシンプルな式で表現してしまうなんて…。）

八代：そういう意味で、天気予報には、100年後のある日ある時刻の天気をぴたりと当てる方法はないということが、証明されてしまっているのです。原理的にこういう予測っていうのは限界があるということはわかっている。けれども、それでも天気予報として、明日の天気だけでなく明後日の天気、さらに３日後の天気も当たるようにするには、まだやれることがあるということが、今、多くの人たちが研究し続けていることなんです。
（ローレンツの方程式によって、予測には原理的な限界があるということがわかっていても、天気予報の精度を上げるために、世界中で多くの人たちがこの瞬間にも努力している。大変だけれども、大切な研究だな、と思いました。）

次回は、アンサンブルをどのように用いてより正確なシミュレーションを目指したかということについて、またスーパーコンピュータを利用した研究のこれからについてうかがいます。